Stretch Transform
2011
Stretch Transform is a geometric transformation that distorts a plane in a rubbery way.
The story started when Benedikt Groß asked me to help with a project. He was working on MapMap Vauxhall and searched for a way to distort a map of London by moving a bunch of points to another location. The rest of the map should move accordingly without producing corners. I did some experiments and got to the following algorithm which I will explain in detail.
But first, play around with it to get an impression of how it's behaving.
- Click and drag somewhere on the grid to add an anchor.
- Drag one of the ends of an existing anchor to move it and select it.
- Click "Delete Anchor" to remove it.
Image morphing
Distorting a grid or maps is one thing you could do with Stretch Transform. But maps are just one kind of image. So, any other image might work as well. Below you'll see a demo where you can mess with my face. If I'll find any pictures of my distorted face in the web, I expect them to have a link to this page attached! :-)
How to use this kind of transformation in your own project?
Download the StretchTransform class from Github. It's a standalone Javascript library which doesn't have any dependencies.
How does this work?
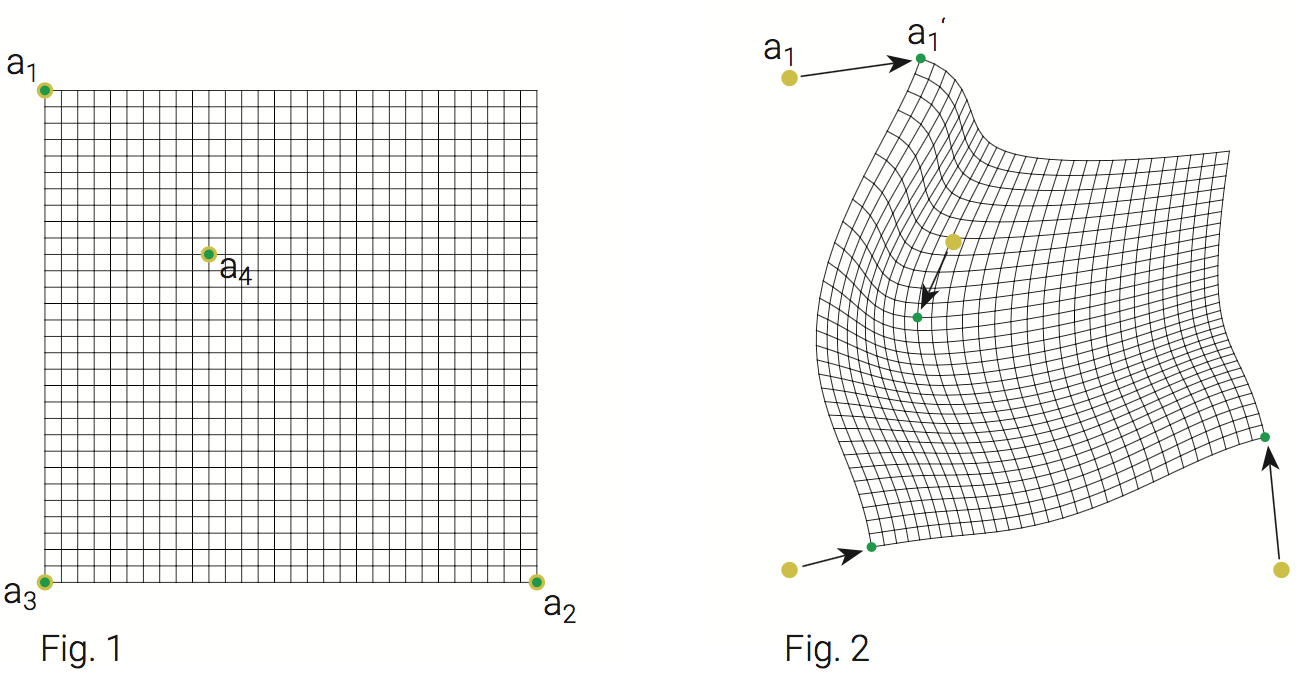
The goal was to have a transformation where an arbitrary number of points (I call them anchors) ai could be set on a plane (original position, Fig. 1) and after moving them to another position ai' (destination position), the plane should be distorted as follows:
- The original point of an anchor should be translated exactly to its target position.
- All points between the anchors should be transformed in a way that the original plane is mapped with as little distorsion as possible and possibly without overlapping (Fig. 2).
- If distorsion is necessary it should be round and not angular.
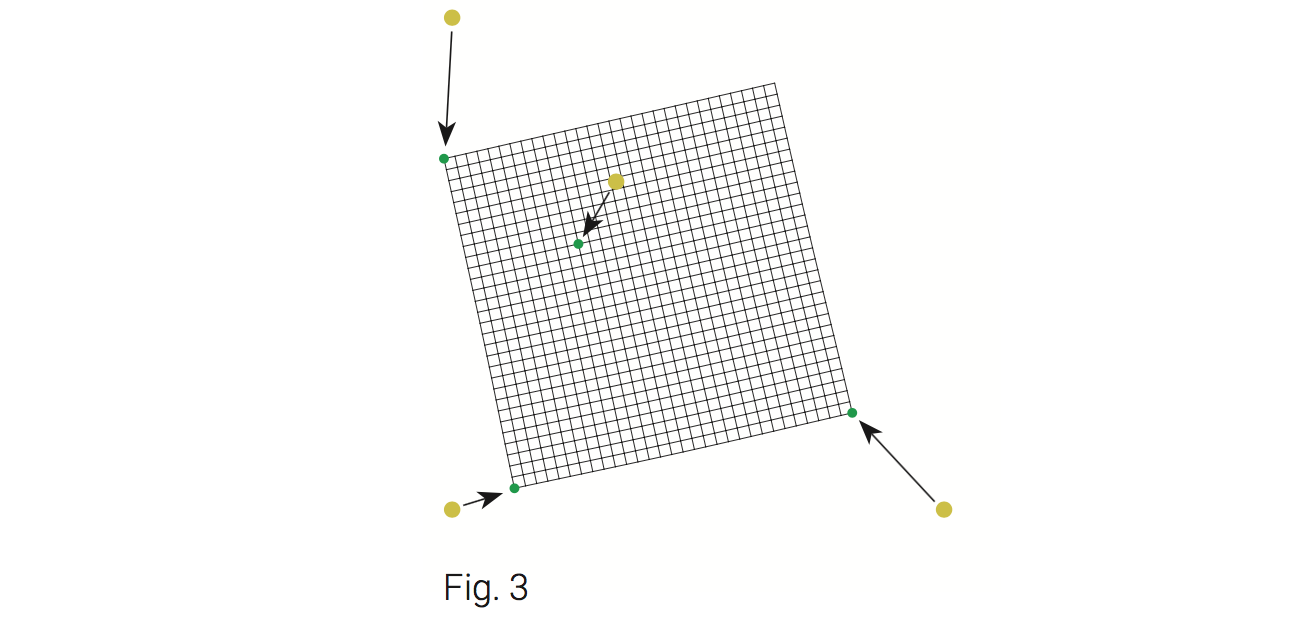
- The transformation should be as close as possible to an affine transformation (Fig. 3).
The algorithm has two main steps: First calculating a transformation matrix Mi for each anchor point, and then applying these matrices in a „weighted“ way to every point that should be transformed.
Step 1
Calculate a transformation matrix Mi for each anchor point. Obviously the transfomation of an anchor point is mainly its translation from position ai to ai'. In order to get such affine transformations as shown in Fig. 3, it is also necessary to calculate a rotation and scaling for the transformation matrix.
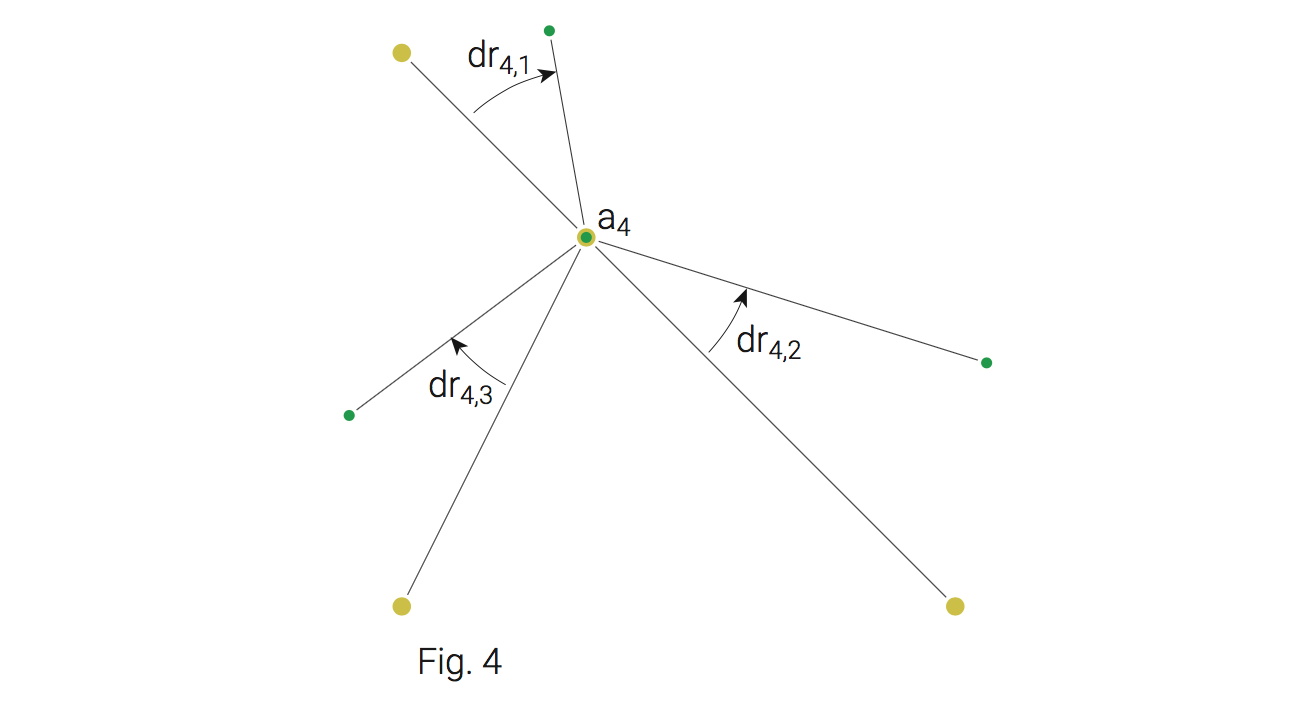
The rotation of an anchor i is calculated as follows:
- Calculate angle ri,j of the vector from ai to aj
- Calculate angle ri,j' of the vector from ai' to aj'
- Calculate difference dri,j of these two angles
- Calculate weighted average of these delta angles. The weighting depends on the distance of the target positions (ai' to aj').
The scaling is done similarly:
- Calculate length li,j of the vector from ai to aj
- Calculate length li,j' of the vector from ai' to aj'
- Calculate quotient qi,j of these two length
- Calculate a weighted „average factor“ of these quotients
Step 2
Apply the anchor transformation matrices in a „weighted“ way to every point p that should be transformed.
- Calculate distances di between p and all original anchor positions ai
- Calculate a weight wi from di so that wi is high when di is low. I used this function: 1 / di2. If di is 0, the point is exactly at an anchor position. In that case, the weight for this anchor will be set to 1, for all other anchors to 0.
- „Normalize“ wi so that the sum of all wi is 1
- Apply anchor transformation matrices Mi to p as follows:
- Calculate vector vi from p to ai
- Calculate vi' by applying Mi to vi
- Calculate weighted difference vector vi* = (vi' - vi) * wi
- Add vi* to p
Acknowledgements
Many thanks to Benedikt for giving me this interesting task to think about.
And also many thanks to David Pritchard who helped me a lot at refining and improving my first version of this transformation. We had a very inspiring talk through email which brought me to new ideas. David also did the very good blog post The artfulness of maps in which he talks about Benedikt Groß' and Bertrand Clercs Metrography project which uses the transformation. There you'll find mainly the same description of the algorithm but expressed in a more mathematical way.
The library is using the great gl-matrix library for vector, matrix and quaternion calculations.